Det er lidt tidligt at gå i souvenirshoppen allerede, synes du ikke? Ørkenen venter
Ad 2 og 3 (fortsat): SPORT
”Jeg gør det hver dag, men det hér sætter ord på det”
En kommentar jeg ofte får, når man forklarer om probabilistisk tankegang (mig inklusive) – det giver potentielt en måde at blive mere komfortabel med usikkerhed og sandsynlighed.
I del 2 af dette blog indlæg (LINK), kiggede vi på hvordan man på en sensibel måde ud fra sin gestalt / patientens præsentation, genererer en differentialdiagnose liste fx i en 2×2 tabel (kan også gøres på anden vis). Udførte vi rendyrket probabilistisk diagnostik, ville vi kun gå efter de diagnoser, der var mest sandsynlige (hvilket ofte er de ikke-tidskritiske). Det at gå efter diagnoser, der er farligst, kaldes ”den prognostiske tilgang” til diagnostik. Som udgangspunkt er vores diagnostik i akutmedicin en blanding af disse to tilgange (prognostisk probabilisme?) – Da vores job er udelukke det mest tidskritiske (og evt som sidegevinst diagnosticere hvad der svarer til lavt hængende frugter), opfordrede jeg jer derfor til at opdele jeres differentialdiagnoselister i tidskritiske og ikke-tidskritiske, og prioritere disse lister efter sandsynlighed.
Efterhånden en begrænset mængde data indsamles om patienten (alder, køn, population, prævalens af sygdom i patientens gruppe, co-morbiditet, risikofaktorer m.v – ofte ift MAPLES delen), kan man ofte hurtigt stryge de fleste af de tentative diagnoser i 2×2 tabellen (evt tilføje enkelte), da sandsynligheden går ned / op for diagnoserne.
Dette er meget intuitivt for os, men det er værd at kigge lidt nærmere på mekanismerne, for at blive bedre diagnostikere (probabilisticians):
Probabilistisk tankegang og ”the threshold model”:
Bayeresiansk / probabilistisk tankegang, er tanken om, at et multiværktøj som implicit eller explicit kan anvendes i tilgangen til enhver patient – Det er udover dette blogindlægs tema, at gå i detaljer med Bayes teori (desuden har flere allerede beskrevet dette bedre end jeg både matematisk: https://www.youtube.com/watch?v=HHIz-gR4xHo, og akutmedicinsk: fx Broom docs fantastiske gennemgang https://broomedocs.com/2016/11/smaccdub-bayes-2016-diagnostic-odyssey/) ).
I en nøddeskal omhandler det dog, at en test ikke kan stå alene uden at kende til præ-test sandsynligheden (fx hvorfor en isoleret D-dimer ikke har nogen betydning; eller hvorfor det ikke er ligemeget, hvad du skriver i henvisningen til den radiologiske undersøgelse). Ved at kende præ-test sandsynligheden, kan testen fortolkes og give post-test sandsynligheden, som danner grundlag for videre diagnostik:
Prætest sandsynlighed x testens vægt = post-test sandsynlighed
Dette kan konceptualiseres i det, der kaldes ”the threshold model” (tærskelmodellen).
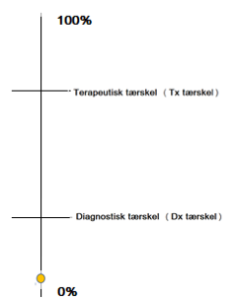
I modellen forestilles hver tentativ diagnose at have en sandsynligheds-linje som afbilledet herover. Procent markørerne illustrerer hvor sandsynlig den tentative diagnose er. Sjældent arbejder man kun med én tentativ diagnose, og derfor skal man forestille sig, at man har flere linjer på en gang, hvor sandsynlighederne bevæger sig op og ned, alt efter hvilke data der indsamles om patienten (note: I princippet har man et uendeligt antal possibilistiske tentative diagnoser, men praktisk talt, kan man, som beskrevet herover, stryge mange tentative diagnoser hurtigt, og stå tilbage med nogle tidskritiske og nogle ikke tidskritiske).
Den gule sandsynlighedsmarkør vil gå op og ned alt efter hvilke data man putter ind om patienten. Før man begynder nogen test, starter markøren på et sted i sandsynlighed (bemærk, at ingen starter ved 0%)., der svarer til patientens baggrundssandsynlighed eller ”Præ-test sandsynlighed” for netop denne tentative diagnose. Denne er givet ved den risikoprofil- og population, samt kliniske spektrum patienten tilhører (ofte sat som ”prævalensen” af sygdommen). Efterhånden som man udfører tests, vil sandsynligheden for diagnosen øges eller sænkes (den gule plet bevæger sig hhv nærmere 100% eller 0%) indtil den asymptotisk nærmer sig ekstremerne (hvilket kun yderst sjældent sker klinisk – jf også is-blok modellen fra del 1) – prøv selv på fx http://www.doclogica.com/
En vigtig pointe at forstå uanset om man anvender probabilisme eller ej er følgende:
Summen af alle tentative differentialdiagnoser = 100%
Det vil sige, at når vi sænker sandsynligheden for én diagnose (fx AKS), vil sandsynligheden for de andre diagnoser stige. På den måde ligger der også en betydelig diagnostisk vigtighed i at ”udelukke” de farligste diagnoser, da de mere sandsynlige dermed bliver endnu mere sandsynlige. Vice Versa kan det være vigtigt, at kende til nogle af de hyppigste non-tidskritiske diagnoser. Vi forstår nu også bedre, hvorfor Zebra-diagnoser (sjældne og tidskritiske), i nogle tilfælde vil kommer mere ind i billedet, når vores flodhest diagnoser (hyppige og tidskritiske), ikke scorer høj sandsynlighed (dette dog med et realistisk skøn ift om zebra-diagnosen eller heste diagnosen er mest sandsynlig – er patienten uforklarligt syg, er forklaringen dog oftere, at vi mangler data (eller gestalt viden) om flodheste diagnosen (fx atypisk præsentation af hyppig diagnose))
Vi efterlader nu threshold modellen kortvarigt, for at forstå nogle af kernekoncepterne i den lidt bedre:

Hvis du har fulgt med indtil nu, så vil jeg sige TAK! – det næste segment er måske tørt og tungt at komme igennem. Jeg fortænker dig ikke i at hoppe det over.
Ørkenvandringer siges dog at være sjælerensende
Hvad er præ-test sandsynligheden, og hvordan finder jeg den for min patent?(4-8)
Hvis vejrudsigten i morgen siger, at det bliver dobbelt så koldt (test), hvor koldt bliver det så?
For at svare på dette spørgsmål, må man kende til base-line – hvor koldt er det i dag? Dette er konceptet om præ-test sandsynlighed.
Præ-test sandsynligheden er defineret som patientens risiko for at have en specifik diagnose, før nogen test udføres på ham/hende. Ofte beskrevet som:
Prætest sandsynligheden = Prævalensen af sygdommen i populationen som patienten tilhører
Spørgsmålet om præ-test sandsynligheden for din patient, besvares derfor først ved at kende til, hvilket klinisk spektrum og population din patient tilhører (Både på individ- og demografi niveau):
| – Alder | <40 år | 40-65 år | >65 år |
| AKS prævalens | 0-2% | 8-10% | 12-19% |
| 0 risikofaktorer* | LR+ 0,17 | LR+ 0,53 | LR+ 0,96 |
| 4 eller derover, risikofaktorer | LR+ 7,4 | LR+ 2,1 | LR+ 1,09 |
* Diabetes, Rygning, hyperkolesterolinæmi, hypertension, arvelighed
- Patientens risikoprofil (individ niveau): patientens ”MAPLES ED” (jf del 2), eller risikoprofil er – alt efter tilstand – mere eller mindre afgørende for patientens præ-test sandsynlighed. Interessant nok, har man i de seneste år begyndt at blive opmærksom på, at vores traditionelle forestilling om ”jo flere risikofaktorer des højere risiko” (eller større præ-test sandsynlighed), ikke er one size fits all (fx om AKS – do risc factors factor: http://www.stemlynsblog.org/simon-carley-risk-factors-really-factor-smaccgold/ ). For nogle tilstande, som AKS, er der studier der peger på, at risikoprofilen alene spiller en væsentlig rolle, hvis man er ung (<40-65år).
Derimod er nogle af de risikofaktorer vi ikke tænker på, oftere en væsentlig spiller – fortsætter vi eksemplet med AKS, kunne dette være misbrug af centralstimulanica (øget risiko for AKS), eller graviditet (øget risiko for bl.a. aortadissektion). Og i virkeligheden, så er de risikofaktorer, vi ikke kender om os selv, eller i videnskaben, uendeligt meget større, end dem vi kender. Samspillet mellem faktorerne er desuden ukendt. Spørger man Richard Body (professor i akutmedicin ved Manchester), er fremtiden formentlig, at vi har en genetisk test profil, der udgør vores risikoprofil. Min pointe er ikke, at risikoprofil ikke er vigtig, men i stedet, at man ikke forblændes af den (for en mere fyldig diskussion jf overstående video ”do risk factors factor”, og http://www.stemlynsblog.org/risk-probability-decisions-emergency-medicine-st-emlyns/ , om ”risk proximity”) .
- Patientens population / Det kliniske spektrum (demografi niveau): Patienten tilhører en bestemt population – dette i form af sin alder, køn, race og kultur. En ung mand fra Danmark med hovedpine har ikke samme risiko for malaria, som en ung mand bosiddende i Afrika med hovedpine. Vi er desuden nødt til at tale om høj- og lavprævalens grupper ift organisation. En patient i almen praksis med mavesmerter har ikke samme incidens af alvorlig sygdom, som en patient i akutmodtagelsen. Og en patient i akutmodtagelsen har ikke samme risiko som en på afdelingen. Patienter filtreres igennem systemet fra lav-prævalent til høj-prævalent (dette er enormt vigtigt at forstå ift valg af tests, risiko for sygdom m.m).
Derudover handler det også om individets (og populationens) sygdomsadfærd, og hvornår de definerer sig syge (af denne grund var vi i Hjørring og Åbenrå FAM altid det mere forsigtige med at udskrive, når en pensioneret landmand kom ind – ud fra personlig erfaring ligger højt for at søge lægehjælp) – jf også modeller som ”health believe modellen”, som mange fra KU vil genkende fra TPK undervisningen. Vær i denne forbindelse også opmærksom på nye systemer, der kan føre til ændret tærskel (= ændret spektrum) for at søge læge – ofte med overdetektion til følge (John Brodersen har talt om dette i bl.a.: https://ebm.bmj.com/content/23/1/1 ). Man har fx i Stockholm indført app’s som KRY (læge på mobilen), hvor man ser, at tærsklen for at søge læge sænkes (folk man ikke ellers ville have set, bliver på den måde visiteret, da KRY ikke kan udelukke mange sygdomme), med det resultat, at koncentrationen af alvorligt syge patienter på akutmodtagelserne sænkes (det absolutte antal alvorligt syge er det samme, men flere ”grønne” patienter = højere støj til signal ratio)
Lad os sige, at du nu kender din patients demografi og individuelle risikoprofil – hvordan får vi så et tal om præ-test sandsynligheden / prævalensen i netop denne gruppe?
Dette er et spørgsmål, der er sværere at svare på. De fleste anvender de 3G’er (Gut feeling, Gestalt eller Guess work: https://broomedocs.com/2016/11/smaccdub-bayes-2016-diagnostic-odyssey/ ), som ofte er godt (særligt jo mere erfaren man er i sit lokale område). Der er dog, som altid ved system 1 tænkning, risiko for bias (fx recency bias, premture closure, anchoring, framing m.m).
For at gøre det mere (pseudo)objektivt / evidensbaseret, findes der tabeller over præ-test sandsynligheden (fx (7) eller http://www.doclogica.com/ , eller jamaevidence serien) – hér skal man dog være opmærksom på, hvor meget stude-populationen som data fra tabellerne er taget fra, passer til din population (mit råd er, at det er det bedste gæt man ofte har, og man må så adaptere ud fra dette tal til sin patient i sin population). Alternativt kan man ved specifikke illness scripts / sygdomme finde CDR’s (clinical decision rules) som estimerer præ-test sandsynligheden.
Oftest bliver det til en hybrid tilgang mellem pseudo-objektive prævalenser, og system 1 / gestalt / mavefornemmelse med de bias der måtte tilhører. Uanset metode, er det altid vigtigt at stille spørgsmålet – ”ville min patient blive deltager i studiet, jeg har mine data fra” eller ”hvordan passer studiet på min patient?” . Til dette kan følgende spørgsmål hjælpe:
- Hvor befinder jeg mig selv? (lav-, moderat-, eller høj prævalens område fx almen praksis Vs specialist center)
- Hvilken tilhører patienten
- Ud fra det generiske kendskab til prævalensen for sygdommen i denne population, hvordan passer dette på MIN patient (og kompenser tilsvarende)
Hvordan ved jeg hvor god testen er? (4, 6, 7)
Først må vi blive enige om, hvad vi mener med ”test”. En test er i virkeligheden enhver form for information, man får om patienten, og den vil derfor ud fra præ-test sandsynlighedens størrelse give en post test sandsynlighed. Traditionelt mener vi med test ”objektiv undersøgelse” eller ”parakliniske test”, men anamnese er ligeså meget en test, som alt andet.
Om en test er god eller dårlig, afhænger af testens evne til at skelne mellem dem, der er syge, og ikke syge (i den population, som vi undersøger). Dette udtrykkes traditionelt som sensitivitet og specificitet (sensitivitet: andel af patienter med positivt testresultat, iblandt dem med den diagnose vi ønsker at finde, specficitet: andel af patienter med negativt testresultat, bilandt dem uden diagnosen vi ønsker at finde). Disse koncepter er ekstremt vigtige at kende til – og vi forstår dem ofte til dels intuitivt. Personligt skal jeg dog altid holde tungen lige i munden, når jeg fortolker dem, og følgende skema og analogi kan måske hjælpe:
| Sensitivitet | Specificitet | Klinisk betydning | Fx |
| ↓ (nær 0%) | ↑ (nær 100%) | ”Patognomiske” symptomer / fund, der primært / oftest findes alene ved den pågældende tilstand (sjældne at finde, men findes de, er sandsynligheden høj for, at man har sin diagnose)
Positiv test: rule in (SpPIN) |
– Becks triade ved tamponade – Skew deviation ved vertigo patient med bagre infarkt |
| ↑ (nær 100%) | ↓ (nær 0%) | Fanger de fleste syge patienter, men også en masse ikke syge
Negativ test: rule out (SnNOUT) |
– D-dimer ved Lungeemboli / DVT |
| ↑ (nær 100%) | ↑ (nær 100%) | Den perfekte test
Negativ: rule out |
– Bedside ultralydskanning for AAA |
| ↓ (nær 0%) | ↓ (nær 0%) | Ubrugelig test
Kan hverken rule in eller out – forvirrer i værste fald billedet |
– |
Det har altid gavnet mig, at tænke min test som et fiske-net, skabt til at fange én særlig type fisk (den særlige sygdom, jeg undersøger). I denne analogi, kan man slutte følgende
- Sensitivitet: Afgør hvor stort fiske-nettet er (hvor stor sandsynligheden er for, at jeg fanger alle de fisk jeg er interesseret i). Jo større sensitivitet, jo flere af ”mine” fisk, fanger jeg, og des mindre bliver sandsynligheden for, at jeg har udeladt nogle af mine fisk, fra nettet. Det vil dermed sige, at har jeg et stort net (høj sensitivt test), kan jeg med rimelig sikkerhed sige, at hvis testen er negativ, er sandsynligheden for at jeg har udeladt nogen, lille (dette kan summeres til huskereglen: SnNOUT – høj sensitiv test, når Negativ, ruler out). Vi ved dog endnu intet om hvor mange andre hav-dyr (sygdomme, der IKKE er den diagnose jeg leder efter). Til dette skal vi bruge Specificitet
- Specificitet: Hvis vi fortsætter analogien med fiskenet herover, vil Specificiteten være præcisionen / præfarencen af nettet til KUN at fange ”mine” fisk (fx kunne man tænke, at netmaskerne er mindre eller større). Jo mere præcist nettets netmasker er (højere specificitet), des større sandsynlighed er der for, at der KUN er min slags fisk i nettet (dette kan summeres til huskereglen: SpPIN – høj specifik test, når positiv, ruler in)
Sensitivitet og specificitet, er dog ofte svære at anvende klinisk (ikke logisk intuitive), , og er desuden population / prævalens afhængige (for større diskussion af problemer med sensitivitet / specificitet, samt NPV og PPV tjek fx https://www.ncbi.nlm.nih.gov/pubmed/9506499 eller Penny Whiting et al: ” How to apply the results of a research paper on diagnosis to your patient”). Kender vi Sensitivitet og specificitet kan man enten via Fagans normogram (https://www.students4bestevidence.net/ebm-for-diagnostic-tests/ ) eller formler, få likelihood ratio’er (LR).
LR er mere intuitive og hjælper indirekte med prævalensafhængigheds problemet, da man er nødt til at tage stilling til præ-test sandsynligheden for at anvende dem. Man skal dog stadig være opmærksom på sygdomsprævalensen i det studie, som LR er kommet fra (og om det passer på din egen). De er kort sagt, blot ”diagnostiske vægte”(7), og alt efter om testen er positiv eller negativ (har patienten symptomet eller ej), opdeles de i hhv LR+ og LR-:
- LR+ (patienten HAR symptomet): hvis patienten har symptomet / fundet (+), hhv øges (>1) eller sænkes (<1) sandsynligheden for en given tilstand tilsvarende LR værdien.
- LR- (patienten har IKKE symptomet): hvis patienten ikke har symptomet / fundet (-), sænkes (<1) sandsynligheden for en given tilstand tilsvarende LR værdien
Forholdet mellem fald / øgning i sandsynlighed kan afbilledes sådan:
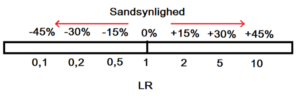
Huskereglen for ændring i sandsynlighed er tenniskamp cifrene: 15-30-45 (hhv LR 2, 5 og 10)
Præ-test sandsynlighed og LR

…skulle jeg have taget en and fra souvenirshoppen?
Stop op
Reflekter
Kriser er ofte muligheder i svøb
Vi har nu begge komponenter i vores formel (Præ-test sandsynlighed x testens vægt (LR) = post-test sandsynlighed). Sætter vi nu de to ting sammen, kan vi nuancere vores fortolkning af LR – Overstående 15-30-45 regel er nemlig god, men er en forsimpling, graden af ændring som en given LR giver, afhænger af præ-test sandsynligheden, som den patient har.. Dette kan man få en fornemmelse af ved følgende tabel (6) (krydsfeltet mellem LR og præ-test sandsynligheden er den procentvise ændring i sandsynlighed) eller diagrammer som dette: https://en.wikipedia.org/wiki/Pre-_and_post-test_probability#/media/File:Pre-_and_post-test_probabilities_for_various_likelihood_ratios.png
| Pretest probability: 5% | Pretest probability: 10% | Pretest probability: 20% | Pretest probability: 30% | Pretest probability: 50% | Pretest probability: 70% | |
| LR = 10 | 34% | 53% | 71% | 81% | 91% | 96% |
| LR = 3 | 14% | 29% | 43% | 56% | 75% | 88% |
| LR = 1 | 5% | 10% | 20% | 30% | 50% | 70% |
| LR = 0,3 | 1,5% | 3,2% | 7% | 11% | 23% | 41% |
| LR = 0,1 | 0,5% | 1% | 2,5% | 4% | 9% | 19% |
Bemærk hér de grønne felter, som indikerer ekstremerne, og illustrerer en vigtig pointe.
Hvis præ-test sandsynligheden er meget høj,
vil selv en god test (LR langt fra 0) ikke kunne udelukke (rule out) diagnosen
Eksempelvis en patient med tordenskrald hovedpine, VAS 10, synkope ifb hovedpine, nakkeryg stivhed og alder >55, vil før CT skanning (Testen) have en ekstrem høj præ-test sandsynlighed for SAH (Ottawa SAH rule). Selv hvis CT skanningen (som hér er en god test med høj LR), er negativ, vil man stadig gå til lumbalpunktur på denne patient).
Vice versa, gælder det, at
Hvis præ-test sandsynligheden er meget lav,
vil selv en god test (LR langt fra 0) ikke diagnosticere (rule in) sygdommen
Bemærk i denne sammenhæng desuden, at man selvfølgelig ikke behøver stille en diagnose, for at indlægge en patient. Har patienten en høj nok post- eller præ-test sandsynlighed (den gule markør på thresholdmodellen er høj nok for en given indlæggelseskrævende diagnose), kan man hurtig nå konklusionen, at man IKKE kan undgå indlæggelse (og arrangere dette med behandling / diagnostik). Faktisk, så kan Thresholdmodellen i stedet for diagnostisk, også omfatte indlæggelse Vs hjem / ambulatorie henvisning (da dette ofte er et mere relevant mål) – jf tabel s 7 i (9)
Nu du kender til LR og thresholdmodellen kan det være, du vil løbe ud og erstatte dit stetoskop (Stetoskopet har faktisk ok LR til visse lungeundersøgelser, men elendig til andre jf tabel herunder – men at ”screene” en population med lav præ-test sandsynlighed) med en lommeregner (evt ultralydsapparat). Der er dog nogle ting du skal være opmærksom på ved LR udregninger:
- Udregning med LR: pga inhomogeniteten af LR, og det faktum, at det er svært at sige hvor præcist en given LR passer til lige præcist din patient (medmindre LR studiet er lavet på dit hospital og i denne gruppe af patienter), må man sige, at LR endnu ikke er skabt til egentlig udregning (mere for at få fornemmelsen af, hvilke risikofaktorer, anamnestiske symptomer, objektive og parakliniske fund, der vægter tungest) – dog vil man se dette blive gjort i bl.a USA
- Addition af LR: Man kan sagtens anvende flere tests på samme tid – således præ-test sandsynlighed x test 1 = post-test sandsynlighed (1). Denne post-test sandsynlighed kan nu anvendes som præ-test sandsynlighed i en ny udregning: post-test sandsynlighed (1) x test 2 = post-test sandsynlighed 2. Problemet herved er dog, at testene ikke må have samme patofysiologi (læs: de skal være uafhængige / måle forskellige områder af patologien bag sygdommen der undersøges). McGee (7), anbefaler på denne baggrund, at man kun adderer 2-3 LR’er (indtil flere studier på området fremkommer).
- Afhængighed af prævalens / prætest sandsynlighed: Som jævnført herover, afhænger testens styrke af præ-test sandsynligheden. Med al dens usikkerhed.
- Sjældent kan enkelte anamnestiske / objektive tests rule out for alt, hvorfor man ofte behøver (bedside) paraklinik, der ofte har bedre LR (fx kan man ved en moderat-høj præ-test sandsynlig patient med mavesmerter ikke rule rumperet AAA ud, uden ultralyd eller andre parakliniske tests)
- Studiet din LR kommer fra skal være generaliserbar / repræsentativ: LR fra studierne skal gerne være på den population din patient tilhører for at give mening. Nogle LR studier udføres fx i ambulatoriet og ikke i akutmodtagelsen. Desuden er der nogle LR studier, er udføres i akutmodtagelsen, hvor testen anvendes på en måde, som vi ikke ville gøre det (fx pro-BNP studier, der undersøgte testen til at skelne mellem hjertesvigt og astma. Denne differentiering er sjældent relevant – i stedet burde den kunne skelne mellem COPD, hjertesvigt og øvrige dyspnø årsager).
- IRR (Inter Rater Reliability) – https://www.students4bestevidence.net/kappa-value/: Typen af læge, der har udført testen i undersøgelsen er formentlig bedre og mere erfaren end dig. Et efterhånden klassisk eksempel er HINTS testen fra Kattah et al 2009 (https://www.ncbi.nlm.nih.gov/pubmed/19762709 ), der viste, at HINTS var bedre end MR skanning til at finde apopleksi i vertigo patienter. I studiet var HINTS undersøgelsen udført af neuro-oftalmologer (denne er dog senere undersøgt med akutmedicinere: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6049818/ ) . Selv under rigtige forhold kan testen have en lav IRR, og optimalt set burde LR studierne parres med kappa-værdier (en oversigt over kappaværdier kan findes i(7)). Så LR på testen i DINE hænder er måske ikke så god som i studie-lægens hænder (løsning: find studier, der er udført at læger af DIN slags fx akutmedicinere – med øvelse stiger IRR. Spørgsmålet om den potentielle LR gevinst er det værd)
Når alt det er sagt, så er LR en effektiv måde at få overblik over hvilke test, der er særligt nødvendige at anvende. Uanset kritikken imod LR, så kan det samme siges om sensitivitet og specificitet og faktisk uanset hvilken metode vi anvender (intuition, possibilistisk, pragmatisk etc), er det samme problemstillinger vi overfor i. Hvis du er hooked på LR, som jeg er, så findes der hjemmesider og bøger med oversigter
- com
- https://canadiem.org/how-to-use-likelihood-ratios/
- Steve McGee, 2017 (7)
- JAMA’s Evidence serie: https://jamaevidence.mhmedical.com/
- com (POCUS)
- org (POCUS)
Optimalt set havde vi en oversigt over LR, demografiske data (hvorhenne udført, hvilket klinisk spektrum, hvilken type læge, hvilken patient præsentation / gestalt), IRR og sensitivtet / specificitet, samt præ-test sandsynlighed for alle target tilstande. Disse studier har der dog ikke været stor interesse i (endnu), og derfor er listerne herover desværre inkomplette (jf mit eksempel i skemaet herunder (kilde: (7) og thepocusatlas.com – bemærk: 1) de fleste fund er lav-sensitive (= fanger ikke alle), men høj specifikke (= når du fanger nogen, er de ruled in) – dvs de er ikke gode til at rule out), hvilket også illustreres i LR, 2) Bemærk, at en LR+ <1 (fx wheeze ved pneumoni), giver en mindre risiko for pneumoni (om end lille))
| Obs diagnose | Symptom / tegn | Population / gestalt | Sens | Spec | LR+ | LR- | Kappaværdi |
| Pneumoni | Krepetition (any) | – Population / præ-test sandsynlighed: Akutmdtagelse, international – Gestalt:patient med feber og hoste- Undersøger: Læge UNS |
19-67 | 39-96 | 2,3 | 0,8 | 0,21-0,65 |
| Wheeze | 10-36 | 50-85 | 0,8 | Non significant (NS) | 0,43-0,93 | ||
| Perkussion dullness | 4-26 | 82—99 | 3,0 | NS | 0,16-0,84 | ||
| Egophoni | 4-16 | 96-99 | 4,1 | NS | ? | ||
| Bronchiale respirationslyde | 14 | 96 | 3,3 | NS | 0,19-0,32 | ||
| Nedsat luftskifte ved st.p | 7-49 | 73-98 | 2,2 | 0,8 | 0,16-0,89 | ||
| Subpleural consolidation and / or focal B-lines på UL | 92 | 94 | 15,3 | 0,09 | ? | ||
| Alle vitalparametre normale | 3-38 | 24-81 | 0,3 | 2,2 | ? | ||
| SAT <95%
TP (>37,8) RF (>28) |
33-52
16-75 7-36 |
80-86
44-95 80-99 |
3,1
2,2 2,7 |
0,7
0,7 0,9 |
? | ||
| Prognostisk score (CURB-65) – prediction of hospital mortality | 0 : 0-16
1: 3-38 2: 17-51 3: 13-61 4: 4-35 5: 1-12 |
0 41-92
1 2 3 4 5: 99-100 |
0: 0,2
1: 0,5 2: NS 3: 2,6 4: 5,9 5: 11,1 |
– | ? | ||
| KOL | Tidlig inspiratorisk krepetition | – Population: ? – Gestalt:?- Undersøger: Læge UNS |
25-77 | 97-98 | 14,6 | NS | ? |
| Wheeze | 13-56 | 86-99 | 2,6 | 0,8 | 0,43-0,93 | ||
| Effusion | Pleural rub | – Population / præ-test sandsynlighed: Akutmdtagelse, international – Gestalt: ?- Undersøger: Læge UNS |
76 | 88 | 6,5 | 0,3 | 0,02-0,51 |
| Nedsat luftskifte ved st.p | – pop | 88 | 83 | 5,2 | 0,1 | 0,16-0,89 | |
| UL fund uden præcis definition (Ingen præcis definition (anechoic fluid above diaphragm (spine sign)) | – Population: Akutmdtagelse, international – Gestalt: ?- Undersøger: radiologer og non-radiologer |
94 | 98 | 47 | 0,06 | ? |
I et forsøg på at komme udenom nogle af problemerne herover ved enkelte LR (og diagnostisk usikkerhed i det hele taget), har man opfundet CDR’s (Clinical Decision Rules):
CDR – Clinical Decision Rules
CDR’s er et forsøg på at kombinere de bedste LR værdier for at skabe en højere LR. Dette er særlig godt ved tilstande, hvor de individuelle LR værdier ikke er så stærke, som fx ved lungeemboli (Wells score), eller hvor samspillet mellem forskellige symptomer er tvetydigt. For en dybere gennemgang af CDR’s anbefales fx https://emergencymedicinecases.com/episode-56-stiell-sessions-clinical-decision-rules-risk-scales/ , og en liste over CDR’s kan findes på https://www.mdcalc.com/ eller https://wikem.org/wiki/Clinical_decision_rules_list
For CDR’s skal dog nævnes:
- Bemærk, at ikke alle CDR’s er skabt lige – CDR’s går igennem et livsforløb på 4 niveauer, fra idé (hvilke LR er gode) til validering (virker vores model udenfor vores afdeling) og impact analyse (giver mening at anvende vores eksternt validerede CDR?). For en gennemgang af dette, anbefales – https://www.youtube.com/watch?v=-goLNbdp27M (sketchy EBM, video serie om ”clinical decision instruments”)
- Stort set de samme begrænsninger gælder for CDR som for LR, og altafgørende er, at CDR’en er lavet på den population, som din patient tilhører (”lever min patient op til inklusionskriterierne i det studie, som CDR’en er lavet på?) (står oftest øverst ved mdcalc.com, under CDR’en)
- CDR’s er af mange typer (Rule out (høj sensitive jf herover), diagnosehjælp, eller prognose / behandlingshjælp) – jf også mdcalc eller https://emergencymedicinecases.com/episode-56-stiell-sessions-clinical-decision-rules-risk-scales/ , der beskriver regler som ”one sided” (enten høj specifikke eller sensitive), eller ”two sided” (både høj specifikke og sensitive)
| CDR | Type | Population | Evidence level | Obs |
| Pneumoni: CURB 65 https://www.mdcalc.com/curb-65-score-pneumonia-severity |
Prognostisk | ED patients | 4 | |
| AKS: HEART score https://www.mdcalc.com/heart-score-major-cardiac-events |
Probabilistisk / diagnostisk hjælp | ED patients > 21 år, uden høj risiko fund (jf mdcalc) | 4 | |
| STEMI ækvivalent LBBB: Modificerede Sgarbossa kriterier https://www.mdcalc.com/sgarbossas-criteria-mi-left-bundle-branch-block eller https://lifeinthefastlane.com/ecg-library/basics/sgarbossa/ |
Probabilistisk / diagnostisk hjælp | Jf mdcalc | 2-3 | |
| Lungeemboli: Wells score for LE | Probabilistisk / diagnostisk hjælp | Klinisk mistanke om LE i ED eller sengafsnit population | 4 | – Skal ikke anvendes ved alle per automatik brystsmerte. Og dyspnø patienter (jf mdcalc) – Skelner ikke mellem alvorligheden af LE |
| DVT: Wells score for DVT https://www.mdcalc.com/wells-criteria-dvt |
Probabilistisk / diagnostisk hjælp | Klinisk mistanke om DVT, ED population / ambulatorie | 3-4 | Obs: ej valideret på sengeafsnit |
| Canadian Syncope risk score https://www.mdcalc.com/canadian-syncope-risk-score |
Probabilistisk / diagnostisk hjælp | ED population, > 16 år, <24 timer fra synkope (jf mdcalc) | 3 | https://www.resus.com.au/2018/07/24/syncope-rules/ |
| Ottawa SAH rule
https://www.mdcalc.com/ottawa-subarachnoid-hemorrhage-sah-rule-headache-evaluation |
Rule out | Jf mdcalc | 3-4 | Meget specifikke inklusions- og eksklusions kriterier |
| Canadian C-spine rule
|
Rule out | 3-4 | C-spine er tiltagende kontroversielt (jf bl.a. norsk, sydafrikansk og nyudkommet dansk holdningspapir) | |
| Klinisk vigtig knæ-fraktur: Ottawa knee rule
|
Rule out | Knæsmerter / ømhed efter traume og alder >2 år, <7 dage siden | 4 | Jf specifikationer på mdcalc |
| Ottawa Ankle rule | Probabilistisk / diagnostisk hjælp + rule out (two sided) | Jf mdcalc | 4 | |
| Aortic Dissection: ADD-RS
https://www.mdcalc.com/aortic-dissection-detection-risk-score-add-rs |
Rule out | Lav risiko patienter i ED, med aorta dissektion som rule-out differentialdiagnose | 2 | – D-dimer kombination ej eksternt valideret
– Kort follow-up (14 dage) |
Slutteligt står vi tilbage med et gabende spørgsmål, som vi vil vende tilbage til i del 4
Hvor lavt skal post-test sandsynligheden være for at være ”ruled out”?
Endelig ude af ørkenen. Vejen frem er mere lys. Få dig noget vand og søvn.
Vær udhvilet til den sidste strækning